学习下用Google的agent开发工具Agent Development Kit
学习下用Google的agent开发工具Agent Development Kit简称 ADK,看着名字就不一般,冲着JDK的地位去的哈哈
首先我们安装下pom包1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30<dependencies>
<!-- The ADK Core dependency -->
<dependency>
<groupId>com.google.adk</groupId>
<artifactId>google-adk</artifactId>
<version>0.2.0</version>
</dependency>
<!-- The ADK Dev Web UI to debug your agent (Optional) -->
<dependency>
<groupId>com.google.adk</groupId>
<artifactId>google-adk-dev</artifactId>
<version>0.2.0</version>
</dependency>
</dependencies>
<build>
<plugins>
<plugin>
<groupId>org.apache.maven.plugins</groupId>
<artifactId>maven-compiler-plugin</artifactId>
<version>3.14.0</version>
<configuration>
<compilerArgs>
<arg>-parameters</arg>
</compilerArgs>
</configuration>
</plugin>
</plugins>
</build>
这个版本也说明了它还不是个完全体
接下去可以生成一个简单的项目结构1
2
3
4
5
6
7
8project_folder/
├── pom.xml (or build.gradle)
├── src/
├── └── main/
│ └── java/
│ └── agents/
│ └── multitool/
└── test/
然后再multitool中创建个java文件,可以叫 MultiToolAgent.java
注意这里需要使用jdk 17及以上版本
示例代码如下1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121package agents.multitool;
import com.google.adk.agents.BaseAgent;
import com.google.adk.agents.LlmAgent;
import com.google.adk.events.Event;
import com.google.adk.runner.InMemoryRunner;
import com.google.adk.sessions.Session;
import com.google.adk.tools.Annotations.Schema;
import com.google.adk.tools.FunctionTool;
import com.google.genai.types.Content;
import com.google.genai.types.Part;
import io.reactivex.rxjava3.core.Flowable;
import java.nio.charset.StandardCharsets;
import java.text.Normalizer;
import java.time.ZoneId;
import java.time.ZonedDateTime;
import java.time.format.DateTimeFormatter;
import java.util.Map;
import java.util.Scanner;
public class MultiToolAgent {
private static String USER_ID = "student";
private static String NAME = "multi_tool_agent";
// The run your agent with Dev UI, the ROOT_AGENT should be a global public static final variable.
public static final BaseAgent ROOT_AGENT = initAgent();
public static BaseAgent initAgent() {
return LlmAgent.builder()
.name(NAME)
.model("gemini-2.0-flash")
.description("Agent to answer questions about the time and weather in a city.")
.instruction(
"You are a helpful agent who can answer user questions about the time and weather"
+ " in a city.")
.tools(
FunctionTool.create(MultiToolAgent.class, "getCurrentTime"),
FunctionTool.create(MultiToolAgent.class, "getWeather"))
.build();
}
public static Map<String, String> getCurrentTime(
String city) {
String normalizedCity =
Normalizer.normalize(city, Normalizer.Form.NFD)
.trim()
.toLowerCase()
.replaceAll("(\\p{IsM}+|\\p{IsP}+)", "")
.replaceAll("\\s+", "_");
return ZoneId.getAvailableZoneIds().stream()
.filter(zid -> zid.toLowerCase().endsWith("/" + normalizedCity))
.findFirst()
.map(
zid ->
Map.of(
"status",
"success",
"report",
"The current time in "
+ city
+ " is "
+ ZonedDateTime.now(ZoneId.of(zid))
.format(DateTimeFormatter.ofPattern("HH:mm"))
+ "."))
.orElse(
Map.of(
"status",
"error",
"report",
"Sorry, I don't have timezone information for " + city + "."));
}
public static Map<String, String> getWeather(
String city) {
if (city.toLowerCase().equals("new york")) {
return Map.of(
"status",
"success",
"report",
"The weather in New York is sunny with a temperature of 25 degrees Celsius (77 degrees"
+ " Fahrenheit).");
} else {
return Map.of(
"status", "error", "report", "Weather information for " + city + " is not available.");
}
}
public static void main(String[] args) throws Exception {
InMemoryRunner runner = new InMemoryRunner(ROOT_AGENT);
Session session =
runner
.sessionService()
.createSession(NAME, USER_ID)
.blockingGet();
try (Scanner scanner = new Scanner(System.in, StandardCharsets.UTF_8)) {
while (true) {
System.out.print("\nYou > ");
String userInput = scanner.nextLine();
if ("quit".equalsIgnoreCase(userInput)) {
break;
}
Content userMsg = Content.fromParts(Part.fromText(userInput));
Flowable<Event> events = runner.runAsync(USER_ID, session.id(), userMsg);
System.out.print("\nAgent > ");
events.blockingForEach(event -> System.out.println(event.stringifyContent()));
}
}
}
}
这个示例非常简单,就是初始化模型,提供基本的提示词,接下去就是两个简单的工具可供使用,提供城市的时间和纽约的天气
要运行起来需要申请api key,然后写到环境变量里1
2export GOOGLE_GENAI_USE_VERTEXAI=FALSE
export GOOGLE_API_KEY=PASTE_YOUR_ACTUAL_API_KEY_HERE
在这里替换成自己的api key就行
然后运行1
2
3
4mvn exec:java \
-Dexec.mainClass="com.google.adk.web.AdkWebServer" \
-Dexec.args="--adk.agents.source-dir=src/main/java" \
-Dexec.classpathScope="compile"
就可以看到一个简单的运行界面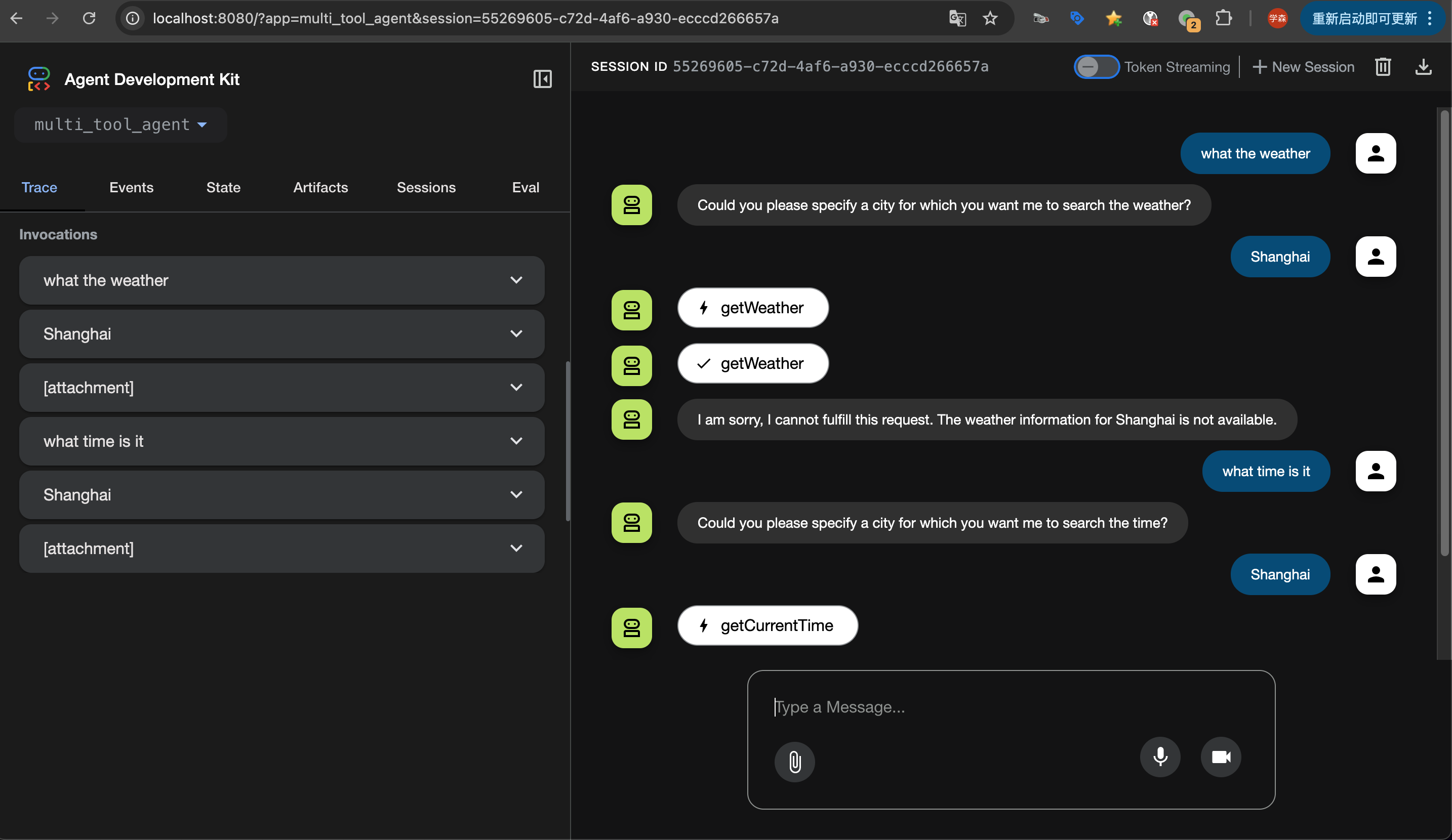
初使用后发现还是比较容易上手,只是后续更深入的还需要好好研究学习