向量数据库学习基础之跳表

发表于 分类于 阅读次数： 阅读次数： Disqus：

在学习向量数据库的时候，发现检索的算法 HNSW 是个比较重要且核心的概念，直接学习（面向小白）可能有一定的门槛，所以我们先通过常见算法的跳表来做个引入
跳表的前置基础就是最常见的序列结构之一的链表，链表的特点是添加插入元素效率非常高，查询检索则需要线性复杂度，比如Java中的hashmap，在jdk1.8以后就把
单纯链表的结构改成了链表和红黑树结合的方式，因为当链表比较长的时候，线性时间复杂度也是个比较慢的方法相比对数时间复杂度，而对于链表，也有直接在它基础
优化而来的跳表结构，跳表是在链表的基础上引入了分层的概念，通过投硬币概率来决定是否生成新层，先用比较通俗的话来讲一下我的理解
因为链表查找只能从前往后一个一个找（单向链表），那么有没有办法可以跳过一些，加速我的查找，那么引入了分层的结构，在更上层以更稀疏的数据链表来索引数据，
举个例子，我原来是一个

1
1 --> 2 --> 3 --> 4 --> 5 --> 6 --> 7 --> 8 --> 9

这样的链表，我要查找8个元素是否存在，那我需要查找八次才能找到
如果我把结构改成

1
2
3
1 --------------> 4 --------------> 7 ---------> null 
|                 |                 |
1 --> 2 --> 3 --> 4 --> 5 --> 6 --> 7 --> 8 --> 9 --> null

变成这样的结构，我现在第一层找最后一个比8小的元素，就是7，然后再到下一层查找，这样我的查找路径就是 1 --> 4 --> 7 --> 8 速度加快了一倍
直观来说这样是能够提升很多查询效率，但是具体怎么实现我们也来看一下
首先定义个简单的Node

1
2
3
4
5
6
7
8
9
public class Node {
    public int data = -1;

    public Node[] forwards;

    public Node(int level) {
        forwards = new Node[level];
    }
}

接下去是SkipList的主体结构

1
2
3
4
5
6
7
8
public class SkipList {
    private static final int MAX_LEVEL = 16;

    private int currentLevel = 0;

    private Node head = new Node(MAX_LEVEL);

    private Random random = new Random();

包含最大层数，当前层数，头结点，跟随机值
生成随机层数参考了redis的zset实现方法

1
2
3
4
5
6
7
private int generateRandomLevel() {
        // 参考redis sorted set 实现
        int level = 1;
        while ((random.nextInt() & 0xFFFF) < (0.25 * 0xFFFF))
            level += 1;
        return Math.min(level, MAX_LEVEL);
    }

接下去先看下

插入元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public void insert(int value) {
        int level = generateRandomLevel();
        if (level >= currentLevel) {
            currentLevel = level;
        }

        Node newNode = new Node(level);
        newNode.setData(value);
        Node[] update = new Node[level];

        Arrays.fill(update, head);

        Node p = head;

        for (int i = level - 1; i >= 0; --i) {
            // 找到应该处在的位置，把前一元素记录为待更新
            while (p.forwards[i] != null && p.forwards[i].data < value) {
                p = p.forwards[i];
            }
            // 对应这一层，更新新的位置p
            update[i] = p;
        }
        
        // 每一层都处理前后链接
        for (int i = 0; i < level; i++) {
            newNode.forwards[i] = update[i].forwards[i];
            update[i].forwards[i] = newNode;
        }
    }

看下图片演示,类似于链表的插入，但是需要处理每一层的前后链接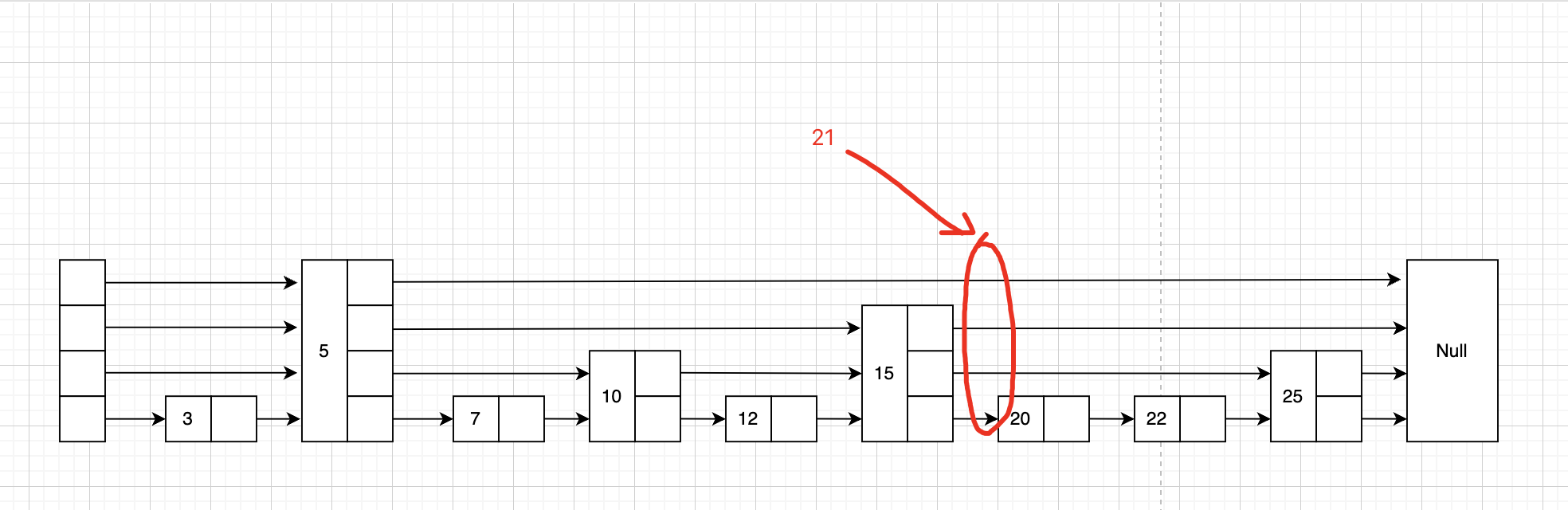

查找元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public Node search(int value) {
        Node p = head;
        // 逐层找到比目标元素小的最后一个元素
        // 然后再往下一层找
        for (int i = currentLevel - 1; i >= 0 ; i--) {
            while (p.forwards[i] != null && p.forwards[i].data < value) {
                p = p.forwards[i];
            }
        }
        // 此时如果前一元素就是目标元素就返回该元素
        if (p.forwards[0] != null && p.forwards[0].data == value) {
            return p.forwards[0];
        } else {
            return null;
        }
    }

也可以看下图里的演示，按红色的线寻找元素

删除元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public void delete(int value) {
        Node[] update = new Node[currentLevel];
        Node p = head;
        // 找到待删除元素的前一元素
        for (int i = currentLevel - 1; i >= 0; i--) {
            while (p.forwards[i] != null && p.forwards[i].data < value) {
                p = p.forwards[i];
            }
            update[i] = p;
        }
        // 判断如果该层有这个元素就更新链接
        if (p.forwards[0] != null && p.forwards[0].data == value) {
            for (int i = currentLevel - 1; i >= 0; i--) {
                if (update[i].forwards[i] != null && update[i].forwards[i].data == value) {
                    update[i].forwards[i] = update[i].forwards[i].forwards[i];
                }
            }
        }
    }

删除操作就类似于插入操作。了解了跳表原理以后其实HNSW就是个在空间层面的跳表