Leetcode 1260 二维网格迁移 ( Shift 2D Grid *Easy* ) 题解分析

发表于 更新于 分类于 ， 阅读次数： 阅读次数： Disqus：

题目介绍

Given a 2D grid of size m x n and an integer k. You need to shift the grid k times.

In one shift operation:

Element at grid[i][j] moves to grid[i][j + 1].
Element at grid[i][n - 1] moves to grid[i + 1][0].
Element at grid[m - 1][n - 1] moves to grid[0][0].
Return the 2D grid after applying shift operation k times.

示例

Example 1:

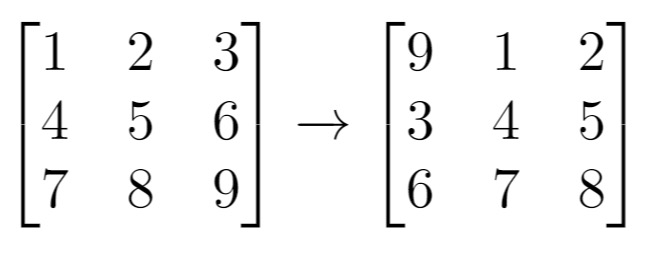
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[9,1,2],[3,4,5],[6,7,8]]

Example 2:

Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

Example 3:

Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
Output: [[1,2,3],[4,5,6],[7,8,9]]

提示

  • m == grid.length
  • n == grid[i].length
  • 1 <= m <= 50
  • 1 <= n <= 50
  • -1000 <= grid[i][j] <= 1000
  • 0 <= k <= 100

解析

这个题主要是矩阵或者说数组的操作，并且题目要返回的是个 List，所以也不用原地操作，只需要找对位置就可以了，k 是多少就相当于让这个二维数组头尾衔接移动 k 个元素

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public List<List<Integer>> shiftGrid(int[][] grid, int k) {
        // 行数
        int m = grid.length;
        // 列数
        int n = grid[0].length;
        // 偏移值，取下模
        k = k % (m * n);
        // 反向取下数量，因为我打算直接从头填充新的矩阵
        /*
         *    比如
         *    1 2 3
         *    4 5 6
         *    7 8 9
         *    需要变成
         *    9 1 2
         *    3 4 5
         *    6 7 8
         *    就要从 9 开始填充
         */
        int reverseK = m * n - k;
        List<List<Integer>> matrix = new ArrayList<>();
        // 这类就是两层循环
        for (int i = 0; i < m; i++) {
            List<Integer> line = new ArrayList<>();
            for (int j = 0; j < n; j++) {
                // 数量会随着循环迭代增长, 确认是第几个
                int currentNum = reverseK + i * n +  (j + 1);
                // 这里处理下到达矩阵末尾后减掉 m * n
                if (currentNum > m * n) {
                    currentNum -= m * n;
                }
                // 根据矩阵列数 n 算出在原来矩阵的位置
                int last = (currentNum - 1) % n;
                int passLine = (currentNum - 1) / n;

                line.add(grid[passLine][last]);
            }
            matrix.add(line);
        }
        return matrix;
    }

结果数据


比较慢